Linear Regression

Overview

선형 회귀(linear regression)은 다수의 데이터가 존재할 때 그 데이터들을 토대로 타당한 기준선을 긋고 새로운 데이터가 들어와도 해당 기준선을 기준으로 예측값을 알아낼 수 있는 기법이다

선형 회귀는 통계학에서 주로 사용되고 있다. 통계학에서 살펴보는 회귀(Regression)의 일반적인 정의는 아래와 같다.

한 종속변수가 하나 이상의 독립변수에 의해 어떠한 영향을 받고 또한 어떠한 관계로 나타나는지 분석하는 기법이 회귀분석이다. 다시 설명하면 종속변수가 독립변수에 의해 어떠한 통계적 관계식으로 나타나는지를 밝히는 것이 회귀분석의 주요 목적이다 (자료조사 1번에서 퍼옴)

단순 선형 모델

위 그림과 비슷하지만 단순화 시킨 예제를 하나 살펴보자. 아래와 같은 간단한 데이터가 있다고 하자.

공부시간 성적
1시간 10점
2시간 20점
3시간 30점

x축이 공부 시간이고, y축이 성적이라고 하자. 인간은 똑똑(?)하니까 쉽게 기존 데이터를 적절하게 관통하는 기준선을 쉽게 그릴수 있다.

그 기준선을 그리는 공식은 아래와 같을 것이다.

y = wx + b

위 공식은 선형 회귀에서 선을 그을때 사용하는 공식으로써 선형 회귀 모델이라고도 부른다. 이는 통계학에서 부르는 용어이고, 딥러닝에서는 가설(hypothesis)라고 부르는것 같다. 실제 통계학에서 사용하는 선형 회귀 모델은 위 공식보다는 조금 항목이 더 있는것 같다.

어쨌든 선형 회귀 모델이기 때문에 직선만 그릴 수 있으며 따라서 1차 방정식으로 가설 모델을 세운다.

위 공식에다 w = 10 , b = 0을 넣는다면 위 표에 맞는 매우 적절한 기준선을 얻을 수 있다. 검증해보자.

Q. 1시간을 공부한 사람의 성적은?

  • 10 * 1 + 0 = 10 > 따라서 성적은 10점이다. 정답이다!
  • 10 * 2 + 0 = 20 > 따라서 성적은 20점이다. 또 정답이다!

이제 4시간을 공부한 학생의 점수를 알아보자. 그런데 기존 데이터에는 4시간을 공부한 학생이 존재하지 않는다. 하지만 우리는 걱정없다. 4시간을 공부한 학생이 몇점을 맞을지 예측이 가능한 모델을 이미 가지고 있지 않은가? 자, 이제 예측을 해보자.

  • 10 * 4 + 0 = 40 > 그래서 40점을 맞을 것이다

이제 실제로 40점을 맞았는지 확인해 보면 될것이다.

이렇게 기존의 데이터에 적절하게 선을 긋고 그에 따른 w값과 b값을 얻어낸 다음에, 새로운 데이터가 들어오면 예측을 하는 방법을 선형 회귀라고 한다.

여기서는 매우 단순한 문제만을 다루었다. 왜 단순하다고 표현했냐면 입력 계수(x)의 값이 하나이기 때문이다. 단순 선형 모델이라고도 부른다. 하지만 우리가 예측해야할 대부분의 경우는 계수가 하나 이상(그것도 엄청 많이...)으로 이루어져 있을 경우가 많다. 이를 다중 변수 선형 회귀(multi variable linear regression)이라고 부르기도 하고, 통계학 에서는 다중 선형 회귀 분석이라고도 부르는 것 같다. 다중 선형 회귀도 선형 모델(가설)이 단순 회귀와 거의 비슷하지만 약간 복잡하다. 추후에 살펴보도록 하겠다.

여기서 문제는 사람은 그래프를 보면 딱 어떻게 선을 그으면 가장 적절한지 직관적으로 알 수 있지만 컴퓨터는 선을 어떻게 그어야 가장 적절하게 그을 수 있는지 모른다는 점이다. 하지만 컴퓨터의 장점이 뭔가? 엄청 계산이 빠르다는 것 아닌가? 이런 장점으로 컴퓨터는 무작위로 선을 그어서 가장 좋은 선을 찾으려고 노력한다. 이런 방법이 통하려면 조건이 있다. 어떤 선이 다른 선보다 더 좋은 선인지 나쁜 선인지 판단할 근거가 있어야 한다는 것이다. 다음 장에서는 어떤 선이 더 좋은 선인지 알아내는 방법에 대해 살펴보자.

선형 모델? vs 비 선형 모델?

인공 신경망 알고리즘을 통해서 하는 작업이 바로 위에서 살펴본 학습 데이터를 적절하게 반영하는 좋은 선찾는 작업을 컴퓨터에게 시키는 것이다. 예제에서는 데이터가 1개뿐이고 매우 이상적이어서 별것 아닌것 같지만, 사진이라던가 소리같은 복잡한 데이터에서 적절한 선들을 찾게 해야 하는데 이건 사람도 정말 만만치 않은 작업이다. 그래도 수없이 반복하면서 계속 좋은 선을 찾도록 시킨다.

사실 사진같은 데이터는 선형 모델이 아니다. 그래서 선형 회귀를 사용해서 풀기에는 조건 자체가 불가능 하지만, 인공 신경망은 다수의 각각의 선형 모델만을 가지고 있는 뉴런(퍼셉트론)을 복잡하게 연결해서 결국에는 비선형 모델을 만들 수 있게 된다.

정확하게 이해되지는 않지만, 인공 신경망은 비선형 회귀를 쓰지 않음에도 공간을 왜곡시켜 결국 선형 모델에 비 선형 데이터를 끼워 맞추는 구조를 갖는다고 한다. 아래 그림을 보는게 이해가 빠를듯...

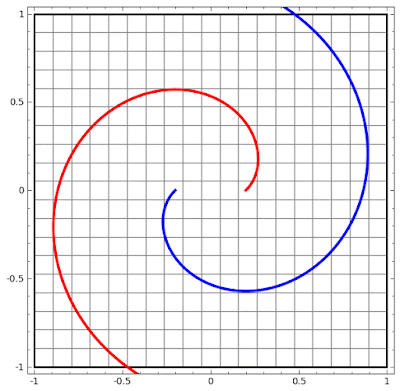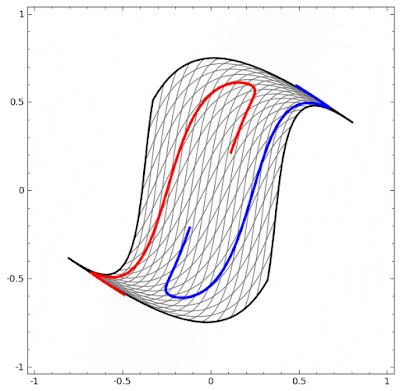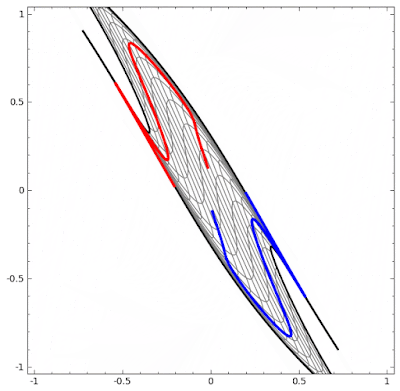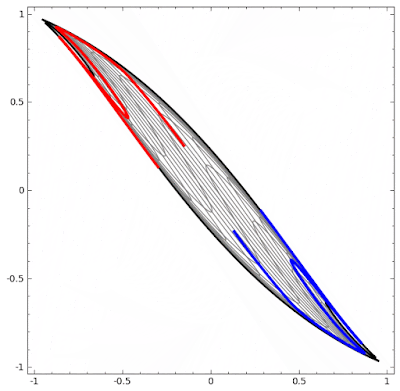
위 그림처럼 데이터 원형 그대로에서는 선형적으로 선을 그을 수 없으니 공간을 구겨서 선에다 맞추는 형태로 선형 회귀를 사용할 수 있게 만들어 버린다. (안되면 되게하라?!)

Q.그냥 비선형 회귀 모델을 사용하면 안될까?
사실 인공 신경망이 이렇게 까지 해서 선형 회귀를 사용하는 이유는, 비선형 회귀를 이용하면 복잡하고 더 성능이 안나와서 일 것 같다. 비 선형 데이터가 그나마 단순하면 비선형 예측 모델로 모델링이 될 수도 있겠지만 엄청 복잡하면 결국 비선형 모델로도 불가능 할 것 같다. 차라리 그럴 바에야 선형 모델을 사용하면서 공간을 비틀어서 선형 모델에 끼워 맞추는게 더 잘된다고 생각하는것 같다.

TODO

  • 비선형 모델에 대해서 더 공부하기

자료조사

results matching ""

    No results matching ""